CEM Models / Standard CEMs
Home Introduction CEM Models CEM Handling Quality Assurance Measurement System MEASAR

 

 

 

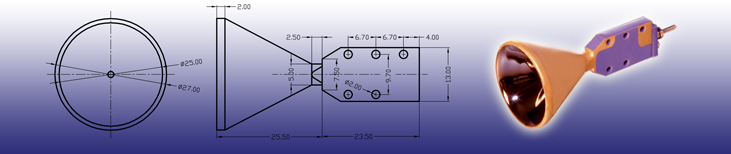
Characteristics of Standard CEMs

 

 

 

 

       
       
  Typical gain at 2.3 kV applied voltage   1 x 10e8
  Typical wall resistance Mohm 200
  Pulse height distribution at 2.6 kV and 3.000 cps % <50
  Dark count rate above a threshold of - 5 mV cps < 0.02
  Maximum count rate cps 5 Mio
  Typical pulse width (FWHM) at 2.3 kV nsec 8
  Operating voltage kV max. 3.5
  Temperature (operating and storage) °C max. 70
  Bake temperature in vacuum °C max. 250
       
       
 
The electro-optical specifications of the Standard type CEMs are valid for all models. Different are the sizes of the entrance funnels, the shapes of the funnels (round, rectangular or square) and the angles between funnels and the CEM bodies. The dark count rates depend on the CEM opening and are at a minimum for smaller openings. Figures 1 - 6 show typical data plots for the Standard CEMs measured with our test equipment.
       
       
       
 
Selection Guide Standard Type CEMs
 

 

Circular Openings

 

Opening Model Model Model

5 mm

 fdsdsf dsds
Model name KBL 5RS KBL 5RS/45 KBL 5RS/90

10 mm

Model name KBL 10RS KBL 10RS/45
KBL 10RS/90
15 mm KBL15RS_45 KBL15RS_90
Model name KBL 15RS KBL 15RS/45 KBL 15RS/90
20 mm
KBL20RS_45 KBL20RS_90
Model name
KBL 20RS
KBL 20 RS/45
KBL 20RS/90
25 mm
 KBL25RS_45 KBL25RS_90
Model name
KBL 25RS
KBL 25RS/45
KBL25RS/90

 

Rectangular Openings

 

Opening
   
Opening
2 x 10 mm 1  

5 x 10 mm

 1
Model name KBL 210   Model name KBL 510
4 x 8 mm 1  

5 x 15 mm

1
Model name KBL 408   Model name KBL 1505
5 x 5 mm 1   10 x 10 mm 1
Model name KBL 505   Model name KBL 1010
 

 

 

 
 

Fig. 1 Typical output pulses at 2.5 kV applied voltage

 
 
Fig. 2 Typical gain characteristic
 
 
Fig. 3 Count rate vs. Applied voltage plot
 
 
Fig. 4 Gain vs. Count rate plot
 
 
Fig. 5 Typical PHD at 2.6 kV (3000 cps)
 
Fig. 6 Typical PHD vs. Applied voltage

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
 
Dr. Sjuts Optotechnik GmbH
  
 

Rudolf-Wissell-Str. 14, 37079 Goettingen, Germany Tel. + 49 (0) 551 209 95 62, Fax. + 49 (0) 551 209 95 63, Email: sjuts@t-online.de

 
             
    User Report  

Courtesy of Dr. Herman Batelaan,

University of Nebraska-Lincoln, USA

    
             
    Why electron counting?        
             
   
The demonstration of absence of force for the Aharonov-Bohm effect (Fig. 1) and the Kapitza-Dirac effect (Fig. 2) happened decades after their predictions [1,2]. In these two experiments, the particle detection was done with Dr. Sjuts electron multipliers.
  
The required temporal resolution of 1 nanosecond is provided by the Dr. Sjuts detector. Given the need to detect the arrival time of individual electron for the first experiment and the low count rate (0.1/s) for the second experiment, the electron had to be counted.

 

Figure 2

   
           
   
     
       
   
   
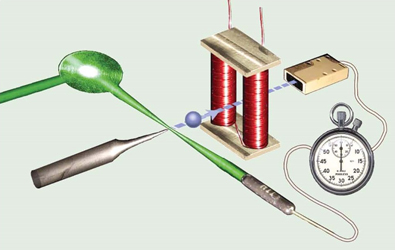
Figure 1. A laser triggers an electron pulse from a sharp needle. The electron pass by magnetized solenoid and even in the presence of a vector potential there is no time delay as measured with a Dr. Sjuts electron multiplier (right top), this means an effect without a force.
 
   
           
   

Both experiments called for nanosecond timing, while for the Kapitz-Dirac experiment this had to be combined with a spatial resolution of mircrometers. A narrow metal slit was placed in front of a channel electron multiplier and translated to obtain the spatial resolution. The comparison to a quantum mechanical calculation showed (inset Fig.2) that the detector had a flat response as a function of position; no background subtraction was needed. Most of the time the laser was off (10 nanosecond pulses with a 50 Hz repetition rate), which meant that the signal had to be filtered out of a strong backgrond with coincidence measurement techniques.

 

      
   

 

      
         
       
A schematic of an electron matter beam (blue) diffracted by the standing wave "grating" of laser beam (green), illustrating that the role of the matter and light are reversed for the Kapitza-Dirac effect
   
    [1] Phys. Rev. Lett. 99, 210401 (2007)        
    [2] Nature 413, 142-153 (2201)